Greeks & IV Made Easy: Delta, Gamma, Theta, Vega, Rho + Implied Volatility

Option traders often invoke the "greeks." What are they, and more importantly, what can they do for you?

In short, the options greeks refer to a set of calculations you can use to measure different factors that might affect the price of an options contract, but they are theoretical in nature. With that information, you can make more informed decisions about which options to trade and when to possibly trade them.

Let's start with the basic definition of each options greek:

• Delta helps you determine how much an option may move if the underlying stock moves by a dollar, but it can also be used to gauge the likelihood an option will expire in the money (ITM).
• Gamma helps you estimate how much the delta might change if the stock price changes.
• Theta helps you measure how much value an option might lose each day to time decay as it approaches expiration.
• Vega helps you understand how sensitive an option might be to large price swings in the underlying stock.
• Rho helps you simulate the effect of interest rate changes on an option.

The Greeks are measurements that estimate how an option’s price should react when one input changes, like the stock price moving, time passing, or volatility changing. Think of them as the option’s “controls panel” while you’re trading.

In this article, any fully bolded paragraphs are meant to be the beginner-friendly explanations.

Implied Volatility (IV)

Implied volatility (IV) is the volatility level “priced in” by the options market. It’s the volatility input that makes a pricing model match the option’s current market price. IV varies by strike and expiration, which is why you’ll see an IV surface (and often a skew/smirk in equities).

Leveraging implied volatility

Implied volatility has a couple of uses beyond vega. Some traders use it to forecast how volatile an underlying stock is expected to be in the future—but it's strictly theoretical. Implied volatility reflected in the price of an option is an inference based on option market participants' expectations of future price moves. Expectations can change depending on upcoming earnings reports, merger and acquisition rumors, pending product launches, etc.

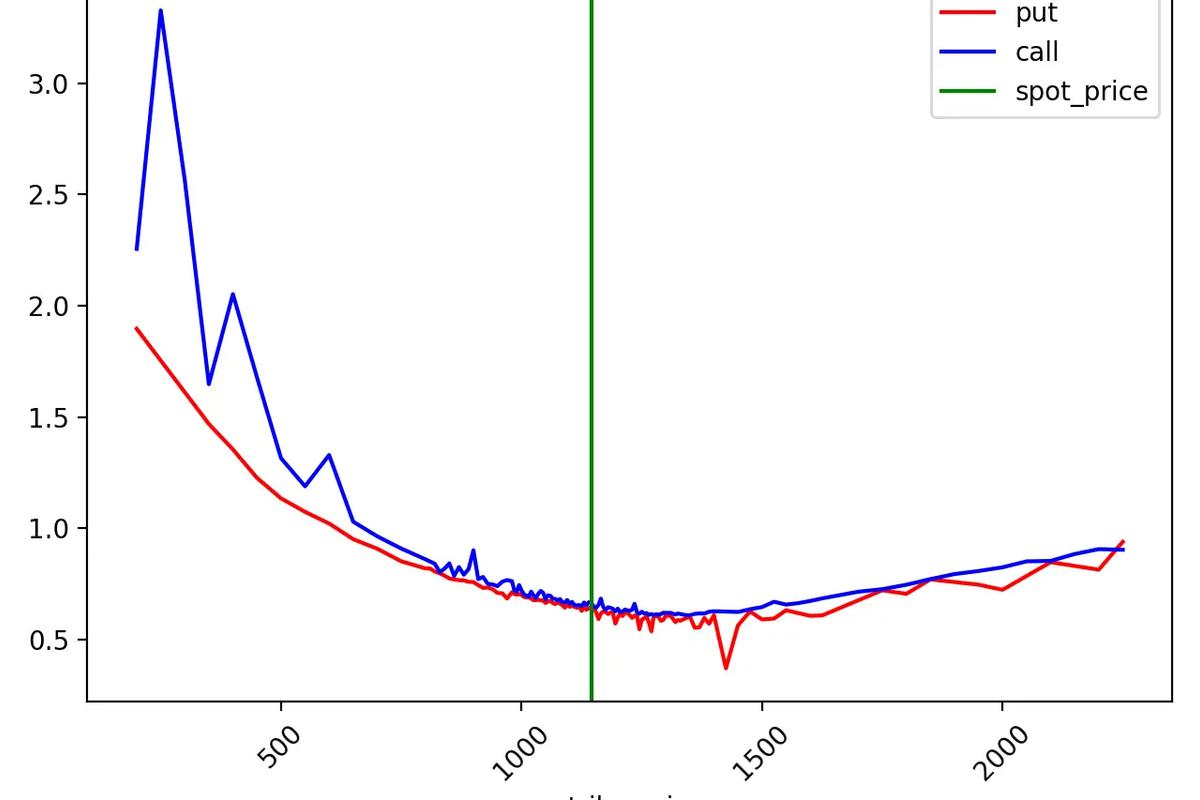
Delta (Δ)

Delta measures how much the price of an option can be expected to move for every $1 change in the price of the underlying security or index. For example, a delta of 0.40 means the price of the option will theoretically move $0.40 if the price of the underlying stock or index changes $1. As you might guess, this means the higher the delta, the bigger the price change.

Traders often use delta to predict whether a given option will expire ITM, meaning its strike price is below (for calls) or above (for puts) the underlying security's market price. So, a delta of 0.40 is taken to mean that, at that moment in time, the option has about a 40% chance of being ITM at expiration. This doesn't mean higher-delta options are always profitable because option buyers have to contest with time decay, which we'll discuss more during the theta section.

Call options

Here are the greeks for call options, which give the buyer the right to purchase the underlying at a set price prior to the designated expiration date:

• A positive delta can range from 0.00 to 1.00.
• At-the-money (ATM) options usually have a delta near 0.50.
• Delta should increase (and approach 1.00) as the option gets deeper ITM.
• Delta of ITM call options will likely get closer to 1.00 as expiration approaches.
• Delta of out-of-the-money (OTM) call options should typically get closer to 0.00 as expiration approaches.

Put options

Here are the greeks for put options, which give the buyer the right to sell the underlying at a set price prior to the designated expiration date:

• A negative delta can range from 0.00 to –1.00.
• ATM options usually have a delta near –0.50.
• Delta should decrease (and approach –1.00) as the option gets deeper ITM.
• Delta of ITM put options will likely get closer to –1.00 as expiration approaches.
• Delta of OTM put options should typically get closer to 0.00 as expiration approaches.

Delta (Δ) measures the sensitivity of the option's premium with respect to that of the underlying asset. For example, with a delta of 0.5 and all else being held equal, a $1.00 change in the underlying price approximately nets a $0.50 change in the option's premium. For call and put options, delta is positive and negative, respectively, because increases and decreases in the spot price are favorable for calls and puts, respectively.

A simple way to think about delta is “how strongly your option acts like the stock.” Higher delta generally means the option reacts more aggressively to stock moves.

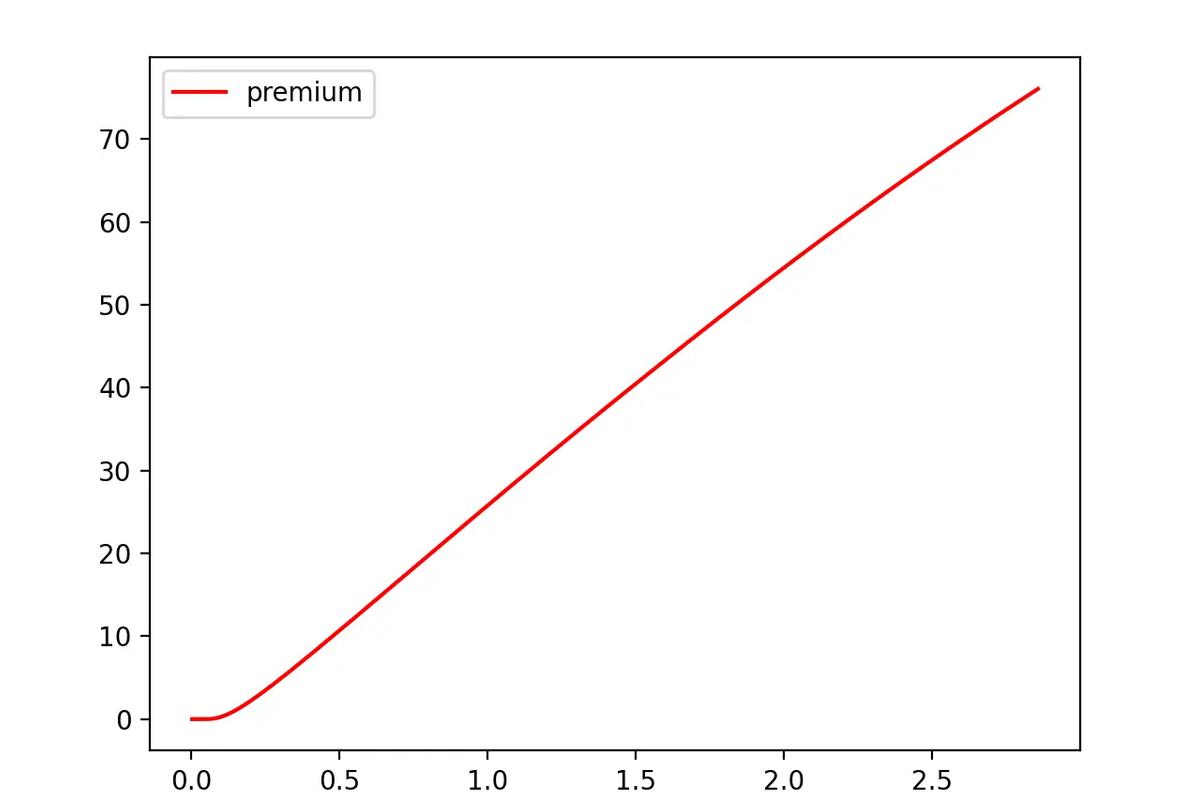
That’s why people say “1 contract controls 100 shares”, your position’s total delta exposure is roughly `Δ × 100` per contract (before considering gamma and IV changes).

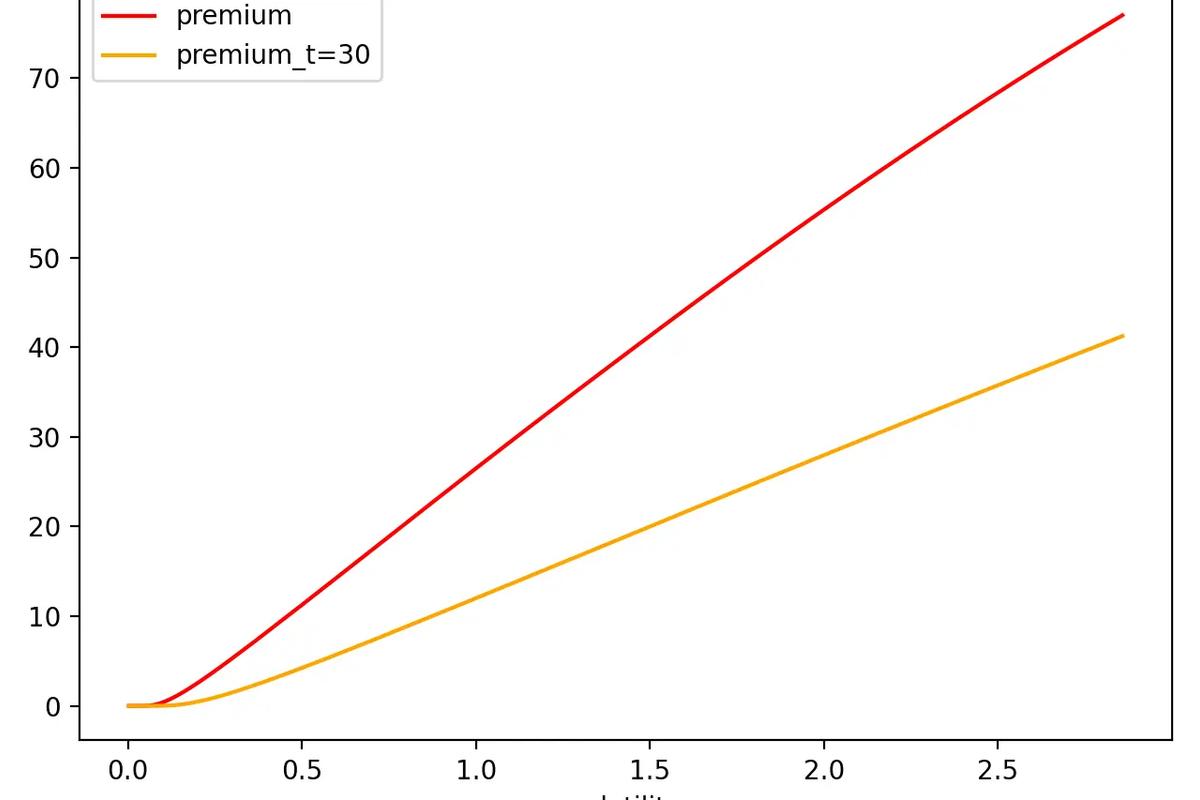
As we can see in the very simple graph above, volatility and premium are almost linearly related. The higher the volatility, the greater premium demanded for the option. Note that other factors such as the spot price (price of the underlying stock), interest rates, and the passage of time can affect this curve. For example, if the time to maturity was instead 30 days, the chart would look like this:

How Options Delta Works: Option’s Price VS Underlying Stock Price

You buy a call option for $1.50 with a delta of 0.50. The share price of the underlying stock immediately shoots higher by $2.00. You can expect your option to gain roughly $1.00 in value — making it $2.50.

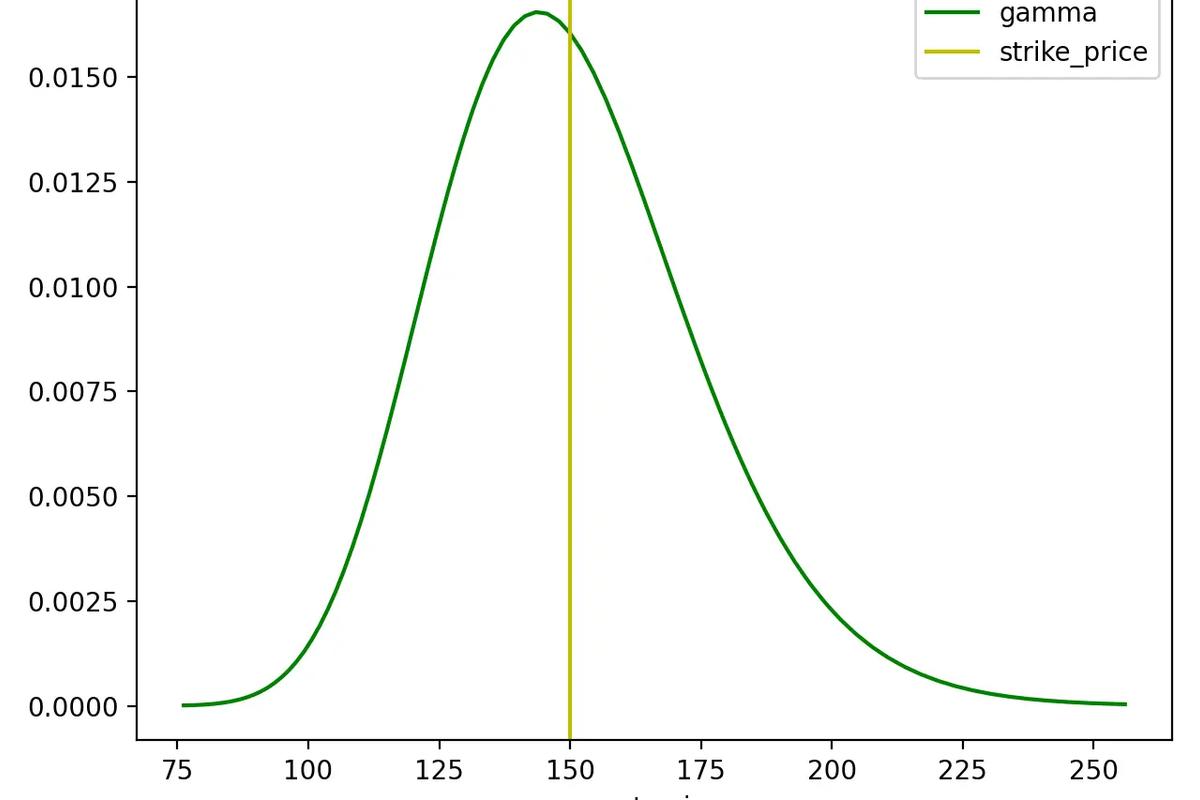
Gamma

Gamma

Where delta is a snapshot in time, gamma measures the rate of change in the delta of an option over time. If you remember high school physics class, think of delta as speed and gamma as acceleration. In practice, gamma is the rate of change in the delta of an option per $1 change in the price of the underlying stock.

In the example above, we used an option with a delta of 0.40. If the underlying stock moves $1 and the option moves $0.40 along with it, the delta is no longer 0.40. Why? This $1 move would mean the call option is now even deeper ITM, so its delta should move even closer to 1.00. Let's assume that as a result delta is now 0.55. The change in delta from 0.40 to 0.55 is 0.15—this is the gamma of the options contract.

Because delta can't exceed 1.00, gamma decreases as an option moves further ITM and delta approaches 1.00. After all, there's less room for acceleration as you approach top speed.

If delta is the “speed” of your option’s price change, gamma is the “acceleration.” When gamma is high, your delta can change fast—so the position can go from calm to chaotic quickly, especially close to expiration near the strike.

As with delta hedging, it is also possible to construct a gamma neutral portfolio, a strategy called delta-gamma hedging. If gamma is high enough, a delta neutral portfolio may still be at risk from movements in the underlying price, since delta may change and the portfolio may require rebalancing with respect to the new value of delta. Delta-gamma hedging also provides protection against larger price movements in the underlying, as delta remains closer to zero for a wider range of prices.

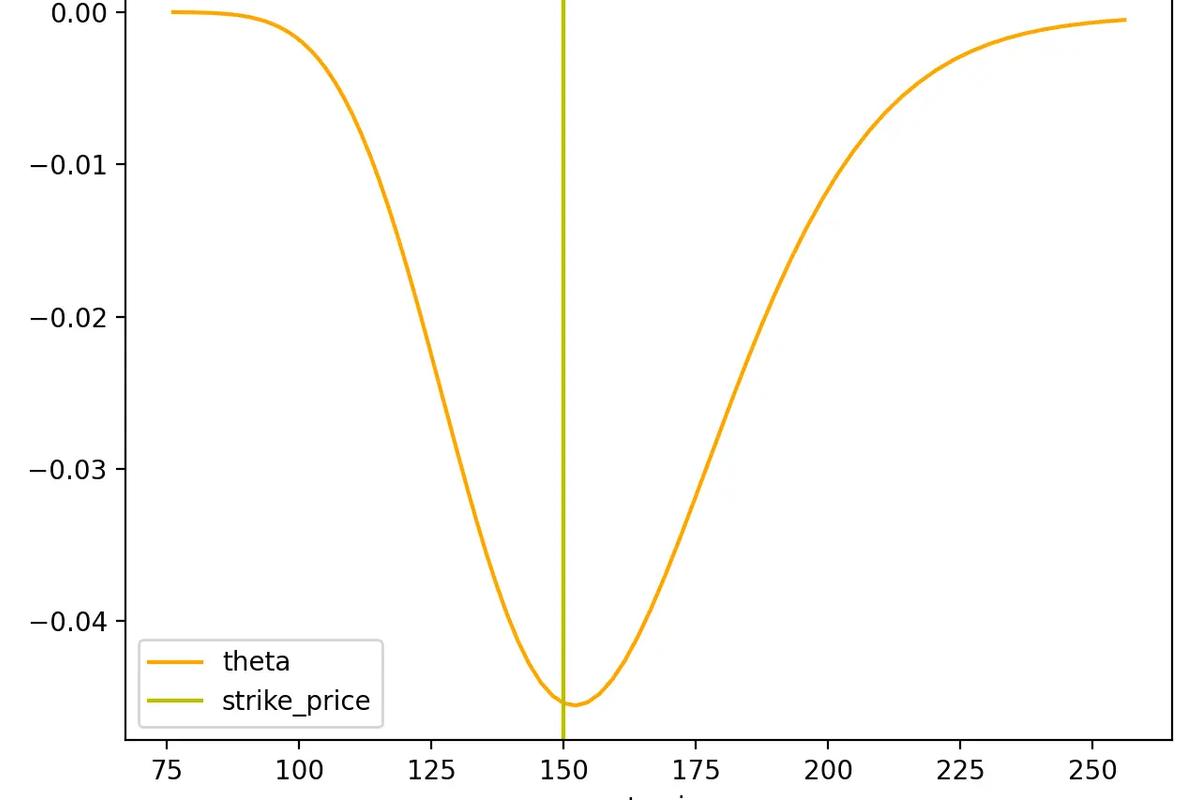
Theta

Theta tells you how much the price of an option should decrease each day as the option nears expiration, if all other factors remain the same. This kind of price erosion over time is known as time decay.

For long calls and puts, theta is always negative, which indicates that the option loses value as time passes. For example, an option with a theta of –0.02 would theoretically lose $0.02 of value every day (including weekends). Like the other greeks, theta doesn't stay the same—it tends to increase closer to expiration, which means options lose value faster as expiration approaches.

For example, a theta of -0.02 means that after one day the option, with all else remaining equal, will be worth $0.02 less than the previous day. Theta is almost always negative for options, because a greater time to maturity generally presents a greater chance for profit.

How theta feels in real trading: Time decay usually isn’t linear, often it’s slower when expiration is far away, and it tends to speed up as expiration gets closer. That’s why short-dated long options can bleed fast if the move doesn’t happen quickly.

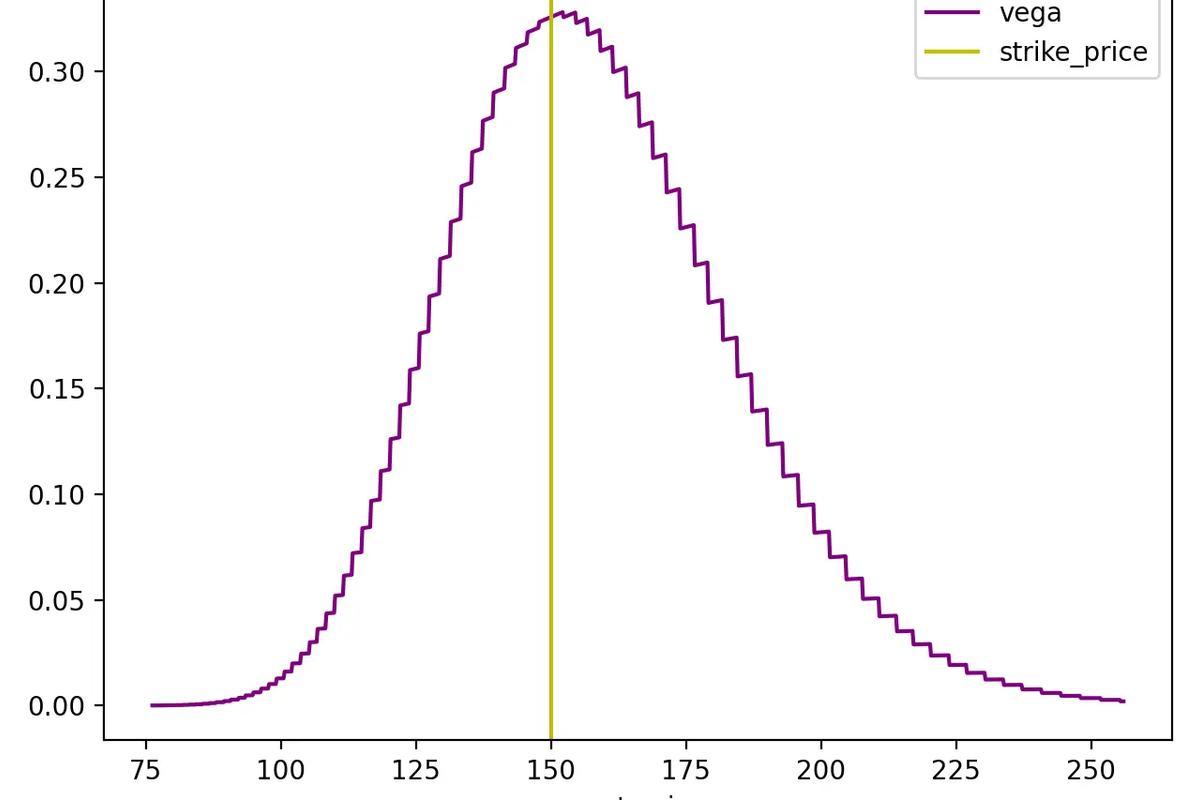
Vega

Vega measures the sensitivity of the option's premium with respect to volatility. If vega is 0.6, then a 1% increase in volatility approximately nets a $0.60 change in the option's premium. Because volatility raises the premium for an option, vega is always positive.

IV crush (common around earnings/news): Before a big event, the market often bids up IV because it expects a large move. After the event happens, IV can drop sharply, so the option can lose value even if the stock moves in the direction you wanted.

More about vega

• Volatility is one of the most important factors affecting the value of options.
• A drop in vega will typically cause both calls and puts to lose value.
• An increase in vega will typically cause both calls and puts to gain value.

Intrinsic vs extrinsic: Intrinsic value is “what the option would be worth if it expired right now.” Extrinsic value is the extra premium for “time + volatility.” Out-of-the-money options are typically all extrinsic, which is why IV changes can hit them harder.

Rho

Rho measures the expected change in the price of an option per one percentage-point change in interest rates. It tells you how much the price of an option should rise or fall if the risk-free interest rate (U.S. Treasury-bills)* increases or decreases.

More about rho

• As interest rates increase, the value of call options will generally increase.
• As interest rates increase, the value of put options will usually decrease.
• For these reasons, call options have positive rho and put options have negative rho.

Consider a hypothetical stock that's trading exactly at its strike price. If the stock is trading at $25, the 25 calls and the 25 puts would both be exactly ATM. You might see the calls trading at, say, $0.60, while the puts could be trading at $0.50. When interest rates are low, the price difference between puts and calls will be relatively small. If interest rates increase, the gap will get wider: Calls will become more expensive, and puts will become cheaper.

Rho is generally not a huge factor in the price of an option, but it should be considered if prevailing interest rates are expected to change, such as just before a Federal Open Market Committee (FOMC) meeting.